|

G R O U P S T R U C T U R E
|
Research Center for Quantum Information
Institute of Physics, Slovak Academy of Sciences
Dúbravská cesta 9, 84511 Bratislava, Slovakia
Tel: (+421 +2) 20910701
|
EXPERIMENTAL PHOTONICS QUANTUM COMMUNICATION GROUP

 Djeylan Aktas
Djeylan Aktas
|


|
SUPERCONDUCTING SPINTRONICS
GROUP
Denis Kochan

 ➫
➫
|
QUANTUM SIMULATIONS AND COMPUTING GROUP

 Andrej Gendiar
Andrej Gendiar
|


|
QUANTUM INFORMATION FOUNDATIONS GROUP
Mario Ziman


|
N E W S |Ξ| ALL NEWS |Ξ|
 01.01.2025 Event
01.01.2025 Event
2025 is Quantum Year
Unesco declared 2025 (among others) as International Year of Quantum Science and Technology. Why? The most probably answer is here [answer]. We are happy to contribute to celebration and spread the quantum truth among all open minds.
May Quantum be with you!
|
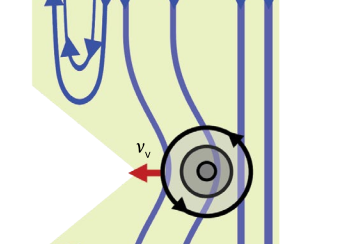 29.05.2025 Expert opinion
29.05.2025 Expert opinion
Low-loss electronics with superconducting diodes
Expertise of our colleague Denis Kochan working in superconducting diodes got crowned by an invited News and Views article in the prestigous Nature Electronics, co-authored with Christoph Strunk (University of Regensburg), they highlighted recent breakthroughs toward low-loss, high-efficiency superconducting diodes—a key step for scalable quantum circuits and energy-efficient electronics.
https://doi.org/10.1038/s41928-025-01388-0
Perex: Two papers report advances in high-efficiency superconducting diodes and multiple-diode rectifiers, which are required for the development of power management systems in scalable quantum circuits.
|
 24.04.2025 Open position
24.04.2025 Open position
skQCI postdoctoral positions in experimental quantum communication technologies
Within the activities of Slovak euroQCI project (skQCI) we are seeking for R3 and R2 researchers experienced in quantum photonics experiment and/or theoretical analyses of quantum communication protocols. Interested candidates pls contact Djeylan Aktas. The positions will start at earliest from July 1st and ends at latest on 31/12/2026. Positions are extendable if agreed. The salaries ranges from 1800-3600 eur depending on the experience and expertize of the candidates.
|
 07.02.2025 Publication [author's view]
07.02.2025 Publication [author's view]
Universal validity of the second law of information thermodynamics
Adiabatic measurements, followed by feedback and erasure protocols, have often been considered as a model to embody Maxwell’s Demon paradox and to study the interplay between thermodynamics and information processing. Such studies have led to the conclusion, now widely accepted in the community, that Maxwell’s Demon and the second law of thermodynamics can peacefully coexist because any gain provided by the demon must be offset by the cost of performing the measurement and resetting the demon’s memory to its initial state. Statements of this kind are collectively referred to as second laws of information thermodynamics and have recently been extended to include quantum theoretical scenarios. However, previous studies in this direction have made several assumptions, particularly about the feedback process and the demon’s memory readout, and thus arrived at statements that are not universally applicable and whose range of validity is not clear. In this work, we fill this gap by precisely characterizing the full range of quantum feedback control and erasure protocols that are overall consistent with the second law of thermodynamics. This leads us to conclude that the second law of information thermodynamics is indeed universal: it must hold for any quantum feedback control and erasure protocol, regardless of the measurement process involved, as long as the protocol is overall compatible with thermodynamics. Our comprehensive analysis not only encompasses new scenarios but also retrieves previous ones, doing so with fewer assumptions. This simplification contributes to a clearer understanding of the theory.
by
Shintaro Minagawa, M. Hamed Mohammady, Kenta Sakai, Kohtaro Kato, Francesco Buscemi
npj Quantum Information 11, 18 (2025)
| +++ |
IMPULZ project No. IM-2023-79 (OPQUT), VEGA 2/0183/21 (DESCOM), APVV-22-0570 (DeQHOST)
|
|
|
S E M I N A R S
| more |
17/06 11:00
Alessandro Bisio (Pavia)
Quantum simulation of scattering processes
|
V I S I T O R S
| history |

26.06-26.07 Che-Pin Hsu (Department of Physics, National Cheng Kung University, Tainan, Taiwan), *mobiQUTE

26.06-26.07 Wun-Hao Kang (Department of Physics, National Cheng Kung University, Tainan, Taiwan), *mobiQUTE

03.07-12.07 João Victor Ferreira Alves (Universidade de São Paulo, Brazil)

08.07-22.07 Vadym Shvydkyi (student)

19.08-13.09 Manuel Schneider (National Yang Ming Chiao Tung University, Taipei, Taiwan) , *mobiQUTE
|
|






|








 01.01.2025 Event
01.01.2025 Event





 29.05.2025 Expert opinion
29.05.2025 Expert opinion
 24.04.2025 Open position
24.04.2025 Open position
 07.02.2025 Publication
07.02.2025 Publication